Calculating distances using a star's pulsations (distance modulus)
Cepheids... and intrinsic pulsating stars.
They seem to live and beat like a resting heart... 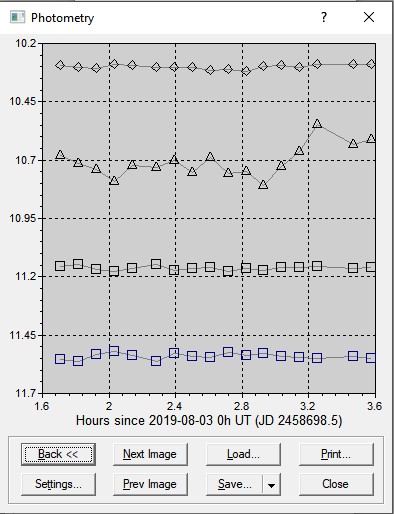
Henrietta Swan Leavitt (1868-1921), who unlocked their mysteries, was able to find a method for estimating distances.
They allowed Edwin Hubble to understand that the great Andromeda Nebula was a galaxy outside our own galaxy. Magic!


Actually...no, Cepheids are really a transition, a phase that some stars go through.
Their fusion in their cores creates pulsations in their outer layers.
A Cepheid is a star 4 to 15 times more massive than the Sun and 100 to 30,000 times more luminous, with a brightness that varies from 0.1 to 2 magnitudes over a well-defined period, between 1 and 135 days. They have left the main sequence and are crossing the instability band caused by helium becoming predominant in their core and beginning to produce carbon, which causes these very regular pulsations.
During their journey, they will cross back and forth across the Hertzsprung-Russell (HR) diagram.
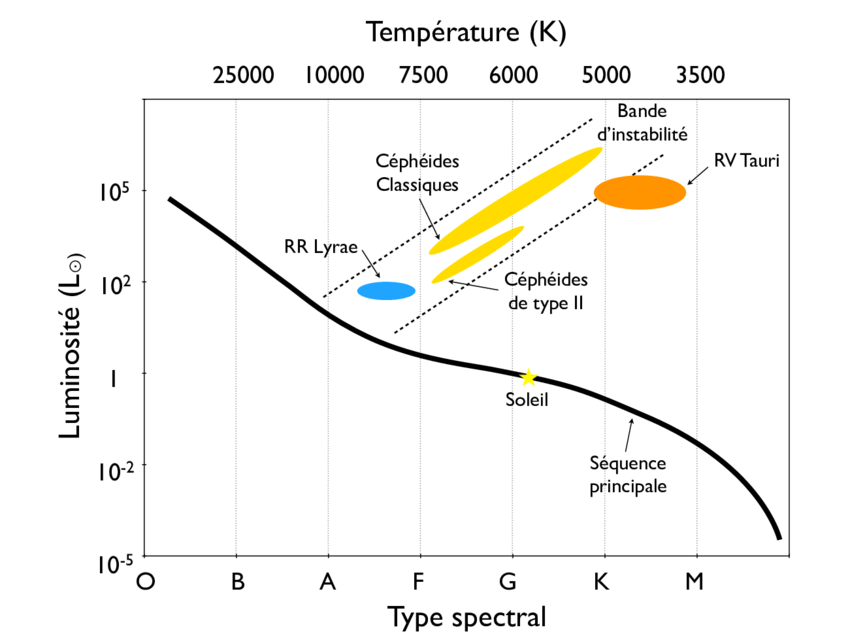
The mystery of the frequency of these pulsations also lies in their size, because the more luminous they are, the slower their pulsations will be.
It is to Arthur Eddington (1926) that we owe the explanation of these pulsations, dubbed the "Eddington Valve" effect. It is thanks to helium that Cepheids pulse regularly; the helium, decaying in the star's core, is ionized several times, making it more opaque. The heat is then trapped. A cycle then takes shape: the more the star is compressed, the more it heats up.

At a certain point during its expansion, it cools and tends to return to its original shape, and the cycle begins again.
The frequency depends on the star's mass; the smaller the star, the faster the frequency, and vice versa for a larger mass.
Therefore, using statistical tables, based on their pulsation frequencies, which can be determined simply by observing them (since their frequency is directly related to the star's mass, the product of its average density ρ, its volume (M = ρV), and then their apparent magnitudes), we can deduce their distances and obtain their absolute magnitudes. Cepheids are thus very useful distance indicators, also called "standard candles."
*However, caution is advised, as other stars are also in the instability band: W Virginis (Type II Cepheids) and RR Lyrae.
These are also Cepheids, but of type II, in other words, old stars with less metallized matter and generally less massive than type I Cepheids. They have longer periods and are often found in globular clusters. RR Lyrae stars, on the other hand, have much shorter periods, and most have spectral type A. They are most often found in star clusters (M3, M13, etc.).
All these families of "intrinsic pulsators" have one thing in common: they are useful as candles for calculating distances based on their pulsation frequencies.
Also, here are some interesting facts about the Cepheids that are among the 100 billion stars in our Galaxy:
- Cepheids are relatively few in number; approximately 1,000 are currently cataloged.
- However, around 20,000 to 35,000 are suspected.
- 5,000 or more could be discovered by the ESA's Gaia mission.
- 40 Cepheids are thought to be visible to the naked eye (among the 6,000 stars in the universe).
- Polaris, the North Star, is the closest and brightest Cepheid (431 light-years).
https://fr.wikipedia.org/wiki/Alpha_Ursae_Minoris
How to use the distance module for classical Cepheids (DCEP)?
1- You need the magnitude observed with a "V" filter.
2- You need the frequency in days, because you can then obtain the absolute magnitude (magnitude of the star seen 10 parsecs from us)
using a calculation: Mv ≃ -2.76 log10 Pd - 1.40
*There is also a website that makes this type of calculation easier:
http://eguruchela.com/physics/calculator/Absolute-Visual-Magnitude-of-Cepheid-Variables-Calculator
3- From this, we can mathematically calculate the distance using the distance modulus.
For example:
Let's take a known Cepheid variable: RX Cam. Its apparent magnitude range is 7.3 - 8.07 using a V-filter.
According to the AAVSO's VSX, this Cepheid has a period of 7.912024 days.
Based on my observations using a V-filter, I obtain an average apparent magnitude of 7.904.
My formula will then be: d (in Parcec) =
So:
So :
So :
So: 2273.2856 PC X 3.26 (pour la conversion en années lumière)= 7410.911 AL
Of course, this calculation is not approximate, and the criteria for photometric quality must be carefully applied across multiple observations from several observatories. The type of star is inherently variable, so unless professional equipment is available, it's difficult to arrive at a precise figure. However, this mathematical approach can still be considered very interesting.
Furthermore, this distance module can be applied to RR Lyrae stars, as we know that, on average, these stars have a relatively stable absolute magnitude varying between 0.6 and 0.7.
Even Type Ia supernovae, which are known to have an absolute magnitude of -19.3 (within a quarter of a magnitude) because the mechanism that produces it is due to a mass threshold, can also benefit from this module to determine their distances at the very beginning of the event, or at its peak.
In fact, the key takeaway is that with a simple distance modulus calculation, once you have the absolute magnitude (magnitude of a star at 10 parsecs) and the precise magnitude (using a V filter), you can obtain a distance.
Again, for a certain level of accuracy, you need to take several readings from multiple observers and average them. But it's still another interesting experiment to try!
References:
https://fr.wikipedia.org/wiki/Henrietta_Swan_Leavitthttps://fr.wikipedia.org/wiki/Expansion_de_l%27Univers
https://astronomia.fr/3eme_partie/variables/varPeriodiques.php
http://www.astrosurf.com/saml/ACCUEIL_suite_1_files/Diaporama%20ce%CC%81phe%CC%81ides_version%20finale_20170715.pdf
https://astronomia.fr/3eme_partie/etoiles_java/calculette.php#:~:text=Consid%C3%A9rez%20par%20exemple%20une%20supernova,la%20distance%20de%20l'astre.
https://fr.wikipedia.org/wiki/Module_de_distance
Sylvie Beaulieu, astrophysicist and head of the Mont Mégantic Observatory: http://omm.craq-astro.ca/
JBD 2020
