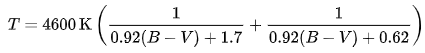Determining the temperature of a star using photometry and spectroscopy.
Photometry and spectroscopy are wonderful tools for studying stars.
It was by analyzing the spectra of black bodies at different temperatures that Wilhelm Wien discovered, in 1893, that light is distributed around a specific wavelength: the emissivity peak, inversely proportional to temperature.
In practice, the maximum reading (spectrum) of a calibrated star's spectrum (A) must be recorded. Photometry can be applied using the same principle, as Johnson/Coussin and Becel filters filter light according to precise scales.
The maximum wavelength (λmax) is the frequency corresponding to the highest point in the spectral curve.
For example, in this spectrum, the λmax corresponds to a value of 5975, which would give a temperature of 4850 K.
* Wikipedia gives a temperature of 4792 K for this star. (https://en.wikipedia.org/wiki/Gamma_Cephei)

The Johnson-Morgan / Cousins / Bessel system
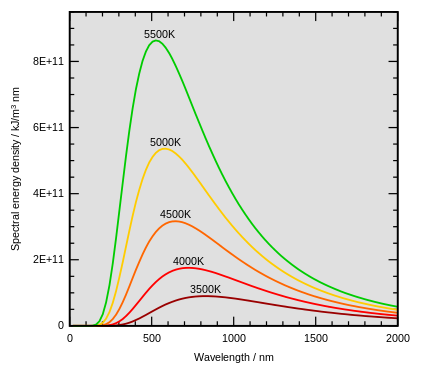
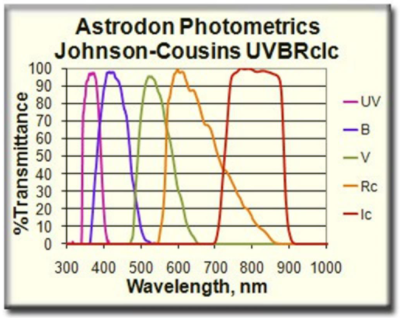
In 1953, Harold L. Johnson and William W. Morgan created the original UBV system, optimized for the photomultiplier tubes of the time. Its aim was to standardize photometry while taking into account older magnitude measurement techniques. Three broad bandwidths were defined: U (365 nm, in the ultraviolet), B (438 nm, in the visible, roughly corresponding to the blue of photographic plates), and V (547 nm, in the visible, roughly corresponding to the wavelength used to calculate visual magnitudes). From its inception, however, the system suffered from certain weaknesses, particularly concerning the limits of the spectral ranges and the small number of standard stars defining the transformations required to convert between the two systems. In 1965, Johnson revised the system, adding R (685 nm, at the edge of the visible spectrum in the red) and I (865 nm, in the infrared).
Ref: https://www.telescopes-et-accessoires.fr/filtre-ccd-johnson-cousins-v-astrodon-coulant-3175mm-c2x30310061
Transmission curve of the original UBV photometric system defined by Johnson and Morgan (1953)
Document: Asiago Database on Photometric Systems.
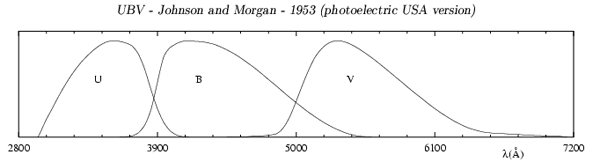
Transmission curve of the UBVRI photometric system defined by Bessel (1990)
UX and BX should be used to calculate the color (U-B). B, G, R, and I should be used for other colors and magnitudes.
Document : Asiago Database on Photometric Systems.
Johnson-Cousins filters
In the early 1990s, Mr. Bessel revised the color gamut to adapt it to the new CCD cameras of the time.
Therefore, in order to produce filters compliant with the UBVRcIc standard, Don Goldman had to design new glass combinations from manufacturers sometimes different from Schott and add interferometric coatings to overcome the limitations imposed by the standard's definition in 1990.
The figure below shows the digitized spectrum of the UVBRcIc filters as provided on the Astrodon company's website.
B-V = Color index of a star:
The simple calculation gives the answer according to the table below:
| Type | Temperature | Couleur | B-V | Dominant rays | Star type |
| W | > 50,000 K | Blue | Star Wolf Rayet | ||
| O | 50 000 à 25 000 K | Blue | < -0,2 | He II,C III, N III, O III, Si V | Ionized helium (HeII) star |
| B | 25 000 à 20 000 K | Blue-White | -0,3 à 0 | H I, O II, Si II, Mg II | Neutral helium (HeI) star |
| A | 10 000 à 7500 K | White | 0 à 0,3 | H I, Mg II, Si II, Fe II, Ti II, etc. | Hydrogen-dominant star |
| F | 7500 à 6000 K | Yellow-White | 0,3 à 0,6 | H I, Ca II, Fe I, Fe II, Cr II, Ti II | Ionized calcium star (CaII) |
| G | 6000 à 5000 K | Yellow | 0,6 à 0,9 | Weak H1, Ca2, and strong metals | Sun-type star |
| K | 5000 à 3500 K | Yellow-orange | 0,9 à 1,5 | metals, Ca I strong, TiO starts at K5 | Metallic strips of neutral metals |
| M | < 3500 K | Red | >1,5 | prominent TiO, numerous metals | Titanium dioxide (TIO) star |
| C | 3000 à 2000 K | Red | >2 | Excess carbon relative to oxygen | Carbon Star |
| S | Red | Zirconium oxide star |
Or, to apply the calculation:
________________________________________________________________________________________
In spectroscopy, it's done using Wien's law.
The application of Wien's law to blackbody radiation is one example of a method for determining the temperature of a star.
(((2.9 · ((10) ^ (- 3)))) / (YMax · ((10) ^ (- 9))))
Therefore, if Lambda Max = 400 Nm, the calculation will be: for a temperature of 7250 Kelvins.
For example:
Betelgeuse has a maximum wavelength (λmax) of 826 nm, and therefore a temperature of 3510.90 K, making it a beautiful orange-red star.
Its neighbor Bellatrix has a maximum wavelength (λmax) of 103.2 nm, and therefore a temperature of over 28,000 Kelvin, making it a blue star.
And our Sun has a maximum wavelength (λmax) of 525 nm, with a temperature of 5523.81 K.
To go further, we can summarize with this table taken from a Paris observation course:
|
T (K) |
2500 |
3500 |
4500 |
5500 |
6500 |
7500 |
8500 |
9500 |
10500 |
11500 |
12500 |
13500 |
14500 |
15500 |
16500 |
17500 |
18500 |
19500 |
|
λ max (nm) |
1156 |
826 |
642 |
526 |
445 |
385 |
345 |
305 |
275 |
251 |
231 |
214 |
200 |
186 |
175 |
165 |
156 |
148 |
On the Paris Observatory website, there is even a simulator to familiarize oneself with this method and these calculations:
https://media4.obspm.fr/public/ressources_lu/pages_corps-noir/spectre-corps-noir-simuler.html
So I wanted to experiment with this law using a few stars like Epsilon Coronae Borealis:
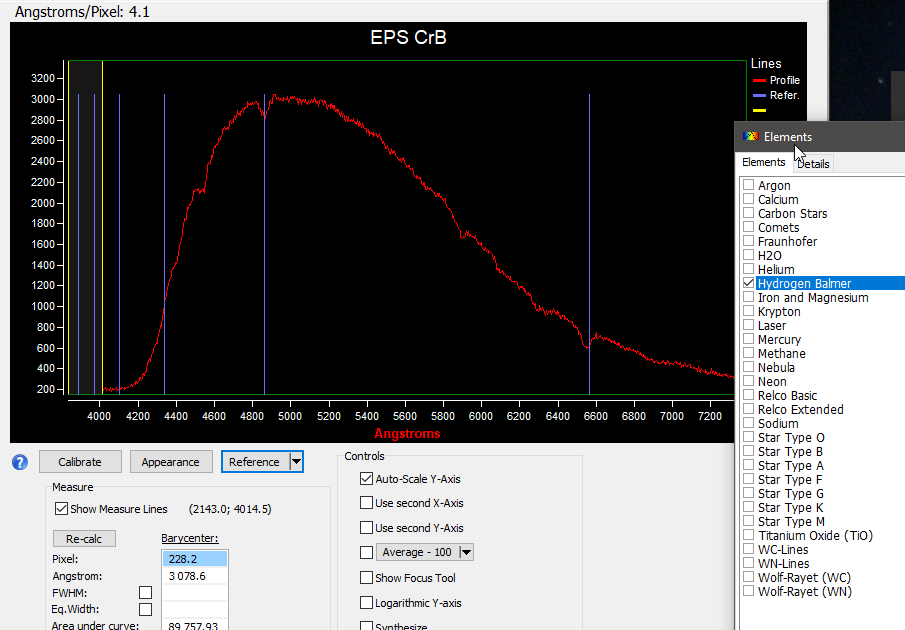
Sur cet autre spectre, Caph de Cassiopé a été fait avec un filtre SA-200 et une lunette ED-80. Le traitement a été fait sur RSpec.
Nous avons ici une lecture max théorique de 4388.8 unités et donc 438.9 Nm
Nous obtenons une température de 6607.43 Kelvin
En fait, sur Wikipédia, Caph de type F2 III, to report an actual temperature of 7079 K, so we are not that far off.
So I repeated the exercise, but this time with my Alpy-600 and processing in BASS Project and its Planck curve module: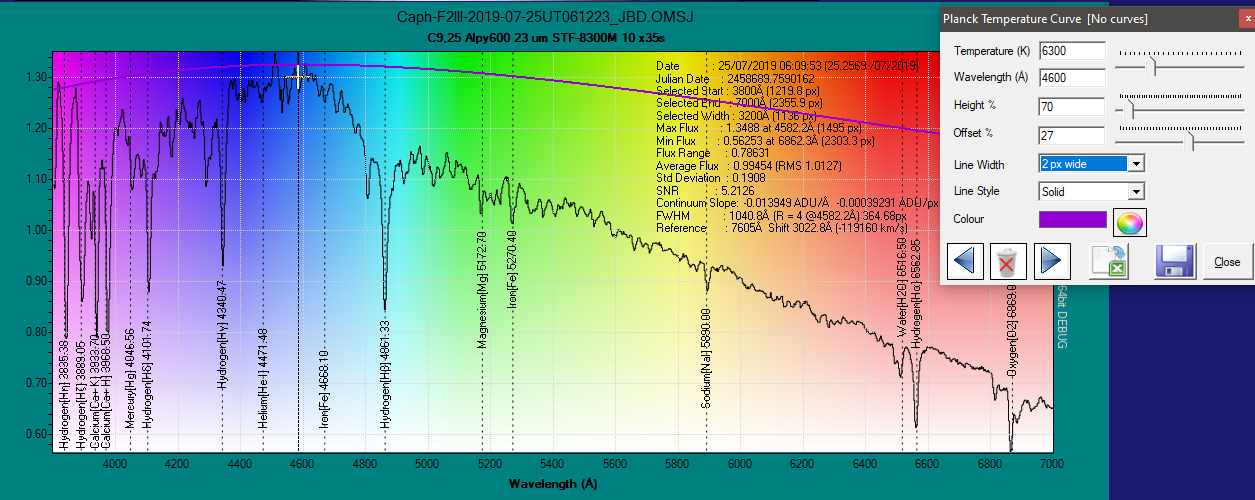
And again, with a lambda around 4600, my temperature hovers around 6300 K.
Betelgeuse:
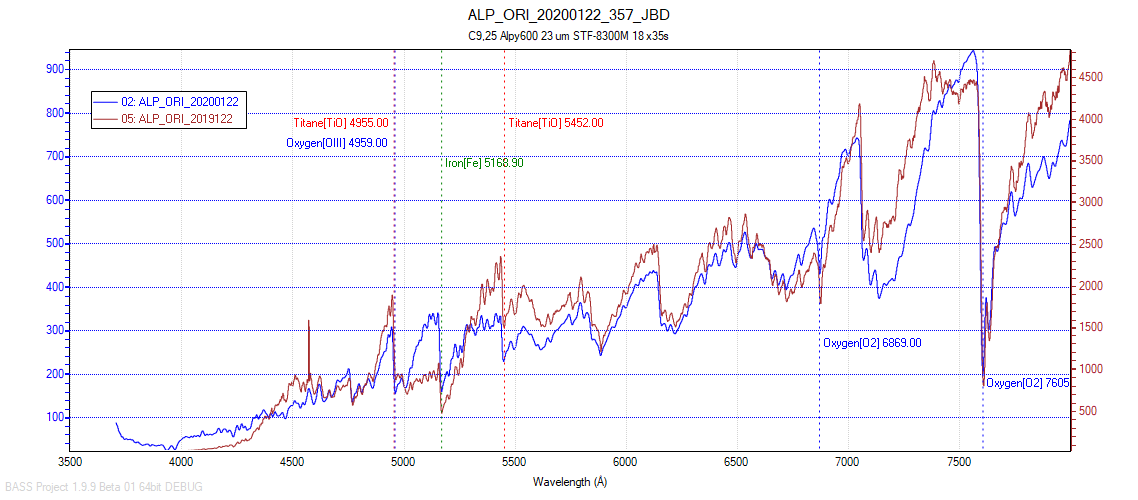
In early 2020, the star Betelgeuse put on quite a show, and I took the opportunity to capture some spectra.
From a compilation of two spectra, I obtained maximum wavelengths of 7400 and 7560, with estimated temperatures of 3916 K and 3833 K, again according to the Planck module of the BASS Project software.
However, Wikipedia states that the official temperature of Betelgeuse is 3600 K. (https://fr.wikipedia.org/wiki/Bételgeuse)
Conclusion
As you've probably gathered, achieving a certain level of accuracy requires averaging several observations, often made by multiple observers and using different telescopes.
But that's yet another fascinating phenomenon to explore!
JBD-2020